Skip to content

Model Comparison with bgmCompare

Source: vignettes/comparison.Rmd
comparison.Rmd

Introduction

The function bgmCompare() extends bgm() to independent-sample designs. It estimates whether edge weights and category thresholds differ across groups in an ordinal Markov random field (MRF).

Posterior inclusion probabilities indicate how plausible it is that a group difference exists in a given parameter. These can be converted to Bayes factors for hypothesis testing.

Boredom dataset

We illustrate with a subset from the Boredom dataset included in bgms.

library(bgms)

?Boredom
data_french = Boredom[Boredom$language == "fr", -1]
data_french = data_french[, 1:5]
data_english = Boredom[Boredom$language != "fr", -1]
data_english = data_english[, 1:5]

Fitting a model 

fit = bgmCompare(x = data_french, y = data_english, seed = 1234)
#> Note: 0.03% of transitions hit the maximum tree depth (1 of 4000).
#> Check efficiency metrics such as effective sample size (ESS) to ensure
#> sufficient exploration of the posterior.

Note: During fitting, progress bars are shown in interactive sessions. In this vignette, they are suppressed for clarity. Sampling can take a while; the progress bars usually help track progress.

Posterior summaries

The summary shows both baseline effects and group differences:

summary(fit)
#> Posterior summaries from Bayesian grouped MRF estimation (bgmCompare):
#> 
#> Category thresholds:
#>                  parameter   mean  mcse    sd    n_eff  Rhat
#> 1 loose_ends(baseline, c1) -0.934 0.002 0.092 2939.560 1.000
#> 2 loose_ends(baseline, c2) -3.798 0.005 0.183 1472.187 1.001
#> 3 loose_ends(baseline, c3) -7.619 0.010 0.339 1225.410 1.001
#> 4 loose_ends(baseline, c4) -0.867 0.002 0.093 3129.955 1.001
#> 5 loose_ends(baseline, c5) -3.813 0.005 0.191 1348.264 1.001
#> 6 loose_ends(baseline, c6) -0.934 0.002 0.092 2939.560 1.000
#> ... (use `summary(fit)$main` to see full output)
#> 
#> Pairwise interactions:
#>                          parameter  mean mcse    sd    n_eff  Rhat
#> 1   loose_ends-entertain(baseline) 0.170    0 0.013 2416.617 1.001
#> 2  loose_ends-repetitive(baseline) 0.127    0 0.012 2662.356 1.000
#> 3 loose_ends-stimulation(baseline) 0.067    0 0.012 2132.079 1.000
#> 4   loose_ends-motivated(baseline) 0.086    0 0.013 2934.346 1.001
#> 5   entertain-repetitive(baseline) 0.137    0 0.012 2021.296 1.001
#> 6  entertain-stimulation(baseline) 0.000    0 0.003 3607.645 1.008
#> ... (use `summary(fit)$pairwise` to see full output)
#> 
#> Inclusion probabilities:
#>                        parameter  mean    sd  mcse n0->0 n0->1 n1->0
#>                loose_ends (main) 0.005 0.071 0.001  3964    15    15
#>                 entertain (main) 0.021 0.143 0.002  3835    81    81
#>                repetitive (main) 0.504 0.500 0.019  1681   300   300
#>               stimulation (main) 0.040 0.195 0.004  3712   129   130
#>                 motivated (main) 0.019 0.137 0.002  3851    72    72
#>  loose_ends-entertain (pairwise) 0.001 0.035 0.001  3991     3     3
#>  n1->1    n_eff  Rhat
#>      5 2419.360 1.056
#>      2 3972.797 1.001
#>   1718  706.161 1.020
#>     28 2995.268 1.000
#>      4 3734.862 1.010
#>      2 1717.353 1.143
#> ... (use `summary(fit)$indicator` to see full output)
#> 
#> Note: NA values are suppressed in the print table. They occur when an indicator
#> was constant (all 0 or all 1) across all iterations, so sd/mcse/n_eff/Rhat
#> are undefined; `summary(fit)$indicator` still contains the NA values.
#> 
#> Group differences (main effects):
#>                parameter   mean    sd  mcse    n_eff  Rhat
#> 1 loose_ends(diff_1, c1) -0.049 0.694 0.020 1167.515 1.003
#> 2 loose_ends(diff_1, c2) -0.004 0.063 0.001 3129.955 1.001
#> 3 loose_ends(diff_1, c3) -0.011 0.159 0.004 2032.234 1.000
#> 4 loose_ends(diff_1, c4) -0.019 0.272 0.007 1348.264 1.001
#> 5 loose_ends(diff_1, c5) -0.026 0.368 0.011 1134.060 1.002
#> 6 loose_ends(diff_1, c6) -0.035 0.501 0.015 1125.242 1.001
#> ... (use `summary(fit)$main_diff` to see full output)
#> 
#> Group differences (pairwise effects):
#>                        parameter  mean    sd mcse    n_eff  Rhat
#> 1   loose_ends-entertain(diff_1) 0.000 0.000    0 3607.645 1.008
#> 2  loose_ends-repetitive(diff_1) 0.001 0.004    0  644.484 1.018
#> 3 loose_ends-stimulation(diff_1) 0.000 0.000    0 2067.428 1.004
#> 4   loose_ends-motivated(diff_1) 0.000 0.000    0 2891.279 1.021
#> 5   entertain-repetitive(diff_1) 0.000 0.000    0  982.504 1.015
#> 6  entertain-stimulation(diff_1) 0.000 0.000    0 2429.237 1.012
#> ... (use `summary(fit)$pairwise_diff` to see full output)
#> 
#> Use `summary(fit)$<component>` to access full results.
#> See the `easybgm` package for other summary and plotting tools.

You can extract posterior means and inclusion probabilities:

coef(fit)
#> $main_effects_raw
#>                    baseline         diff1
#> loose_ends(c1)   -0.9335448  1.353684e-06
#> loose_ends(c2)   -2.5160671  1.913279e-03
#> loose_ends(c3)   -3.7981214  1.746971e-03
#> loose_ends(c4)   -5.0862036  1.586779e-03
#> loose_ends(c5)   -7.6186947 -5.641530e-04
#> loose_ends(c6)  -10.1215955 -2.948219e-03
#> entertain(c1)    -0.8672713 -3.238407e-04
#> entertain(c2)    -2.2442298 -6.052487e-06
#> entertain(c3)    -3.8125399  4.409582e-04
#> entertain(c4)    -5.1708255  1.934664e-04
#> entertain(c5)    -7.0439301  2.585494e-04
#> entertain(c6)    -9.5761797  8.500207e-04
#> repetitive(c1)   -0.1382395 -2.957967e-03
#> repetitive(c2)   -0.6596801 -5.081336e-03
#> repetitive(c3)   -1.0873176 -1.376381e-03
#> repetitive(c4)   -1.8655581  3.552845e-03
#> repetitive(c5)   -3.2533504  8.608963e-03
#> repetitive(c6)   -5.0346164  9.108386e-03
#> stimulation(c1)  -0.5471426 -3.479786e-03
#> stimulation(c2)  -1.7883340 -7.534717e-04
#> stimulation(c3)  -2.5339950 -1.188131e-03
#> stimulation(c4)  -3.6203067 -3.208995e-03
#> stimulation(c5)  -5.1021794 -2.096424e-03
#> stimulation(c6)  -7.0734306 -4.997347e-03
#> motivated(c1)    -0.5573760 -1.671857e-03
#> motivated(c2)    -1.8027889 -6.952556e-04
#> motivated(c3)    -3.2913727  6.448214e-04
#> motivated(c4)    -4.7841676  1.613263e-03
#> motivated(c5)    -6.7826610 -9.152204e-04
#> motivated(c6)    -9.1456487  1.709301e-03
#> 
#> $pairwise_effects_raw
#>                          baseline         diff1
#> loose_ends-entertain   0.16957126  0.0001678142
#> loose_ends-repetitive  0.05813207  0.0217766572
#> loose_ends-stimulation 0.12691674  0.0008670351
#> loose_ends-motivated   0.14100594 -0.0002092935
#> entertain-repetitive   0.06716624  0.0045123472
#> entertain-stimulation  0.10947097  0.0020177958
#> entertain-motivated    0.08596872  0.0043062073
#> repetitive-stimulation 0.05618111  0.0007279903
#> repetitive-motivated   0.13718742  0.0147375246
#> stimulation-motivated  0.10782364  0.0001179359
#> 
#> $main_effects_groups
#>                      group1      group2
#> loose_ends(c1)   -0.9335455  -0.9335442
#> loose_ends(c2)   -2.5170238  -2.5151105
#> loose_ends(c3)   -3.7989948  -3.7972479
#> loose_ends(c4)   -5.0869969  -5.0854102
#> loose_ends(c5)   -7.6184127  -7.6189768
#> loose_ends(c6)  -10.1201214 -10.1230696
#> entertain(c1)    -0.8671094  -0.8674332
#> entertain(c2)    -2.2442268  -2.2442328
#> entertain(c3)    -3.8127604  -3.8123194
#> entertain(c4)    -5.1709223  -5.1707288
#> entertain(c5)    -7.0440593  -7.0438008
#> entertain(c6)    -9.5766047  -9.5757547
#> repetitive(c1)   -0.1367605  -0.1397185
#> repetitive(c2)   -0.6571394  -0.6622207
#> repetitive(c3)   -1.0866294  -1.0880058
#> repetitive(c4)   -1.8673346  -1.8637817
#> repetitive(c5)   -3.2576549  -3.2490459
#> repetitive(c6)   -5.0391706  -5.0300622
#> stimulation(c1)  -0.5454027  -0.5488825
#> stimulation(c2)  -1.7879573  -1.7887108
#> stimulation(c3)  -2.5334009  -2.5345890
#> stimulation(c4)  -3.6187022  -3.6219112
#> stimulation(c5)  -5.1011311  -5.1032276
#> stimulation(c6)  -7.0709319  -7.0759292
#> motivated(c1)    -0.5565400  -0.5582119
#> motivated(c2)    -1.8024413  -1.8031365
#> motivated(c3)    -3.2916951  -3.2910503
#> motivated(c4)    -4.7849742  -4.7833609
#> motivated(c5)    -6.7822034  -6.7831186
#> motivated(c6)    -9.1465033  -9.1447940
#> 
#> $pairwise_effects_groups
#>                            group1     group2
#> loose_ends-entertain   0.16948735 0.16965516
#> loose_ends-repetitive  0.04724374 0.06902040
#> loose_ends-stimulation 0.12648323 0.12735026
#> loose_ends-motivated   0.14111059 0.14090130
#> entertain-repetitive   0.06491007 0.06942242
#> entertain-stimulation  0.10846207 0.11047987
#> entertain-motivated    0.08381561 0.08812182
#> repetitive-stimulation 0.05581711 0.05654510
#> repetitive-motivated   0.12981866 0.14455618
#> stimulation-motivated  0.10776467 0.10788261
#> 
#> $indicators
#>             loose_ends entertain repetitive stimulation motivated
#> loose_ends     0.00500   0.00125    0.13275     0.07450   0.12675
#> entertain      0.00125   0.02075    0.01475     0.03425   0.36950
#> repetitive     0.13275   0.01475    0.50450     0.00650   0.01325
#> stimulation    0.07450   0.03425    0.00650     0.03950   0.00575
#> motivated      0.12675   0.36950    0.01325     0.00575   0.01900

Visualizing group networks

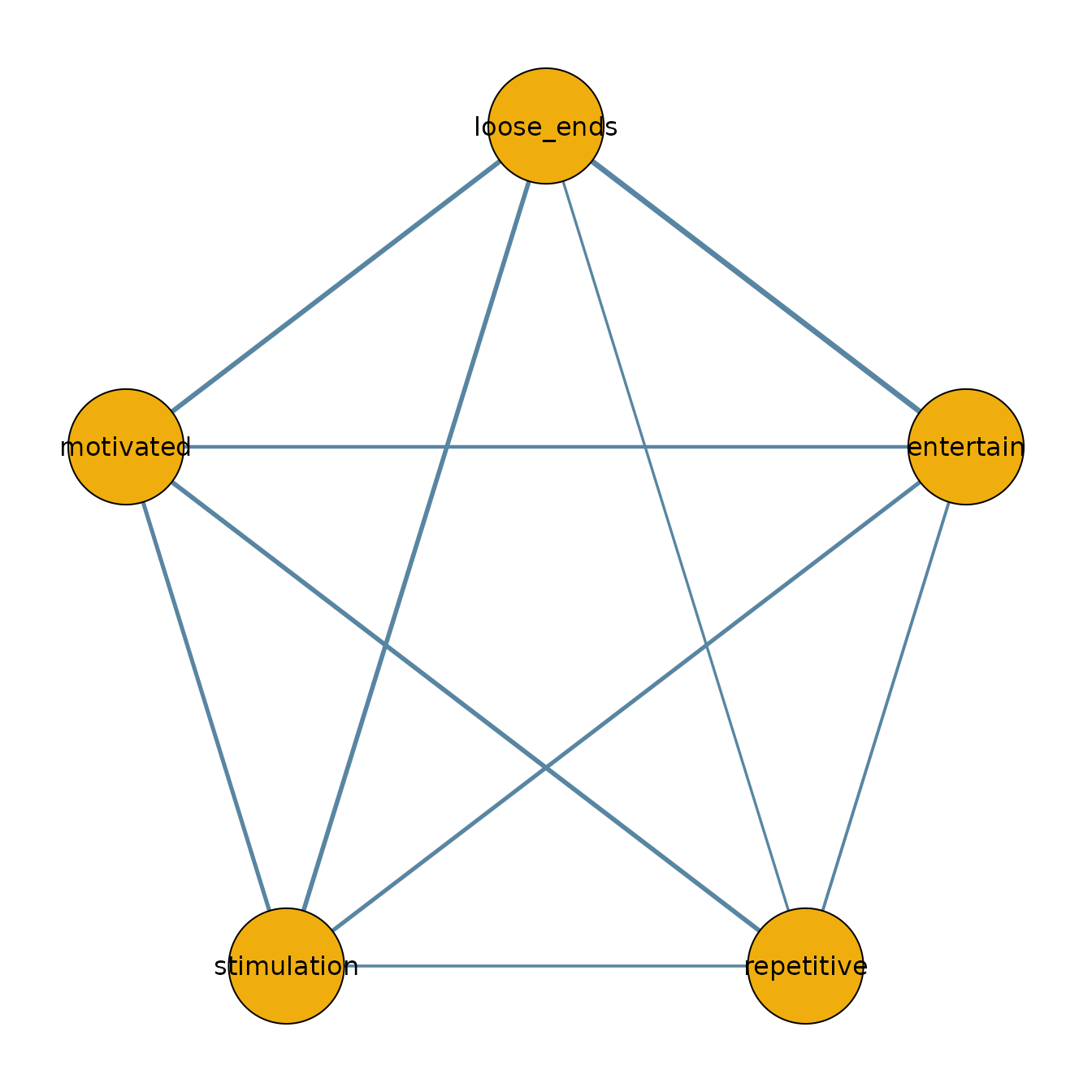
We can use the output to plot the network for the French sample:

library(qgraph)

french_network = matrix(0, 5, 5)
french_network[lower.tri(french_network)] = coef(fit)$pairwise_effects_groups[, 1]
french_network = french_network + t(french_network)
colnames(french_network) = colnames(data_french)
rownames(french_network) = colnames(data_french)

qgraph(french_network,
       theme = "TeamFortress",
       maximum = 1,
       fade = FALSE,
       color = c("#f0ae0e"), vsize = 10, repulsion = .9,
       label.cex = 1, label.scale = "FALSE",
       labels = colnames(data_french))

Next steps

  • For a one-sample analysis, see the Getting Started vignette.
  • For diagnostics and convergence checks, see the Diagnostics vignette.
  • For additional analysis tools and more advanced plotting options, consider using the easybgm package, which integrates smoothly with bgms objects.